재귀함수를 이용하여 알고리즘을 구성하는 경우 많은 문제를 해결할 수 있습니다. 재귀함수와 어떻게 사용해야 하는지 팁을 공유하도록 하겠습니다.

재귀함수
어떠한 함수에서 자신을 다시 호출하여 작업하는 작업방식입니다. 위의 이미지는 방송을 호출할 때 무한화면으로 나와 있는데 이것처럼 이론상 무한으로 재귀함수를 사용할 수 있습니다. 하지만 재귀함수의 공간을 스택 메모리에 담기 때문에 너무 많은 재귀함수를 사용하는 경우 스택 오버플로우로 에러가 날 수 있습니다.
여담으로 재귀함수를 사용하지 않아도 반복문으로 재귀함수처럼 문제를 해결할 수 있습니다. 그럼에도 불과하고 재귀함수를 사용하는 경우는 다음과 같습니다.
- 재귀적인 경우가 더 자연스러운 알고리즘인 경우에 사용한다
- 스택으로 메모리를 이용하기 때문에 변수 사용이 줄어든다
- 코드가 간결해져 가독성이 향상된다
1번의 경우처럼 재귀적인 경우가 더 자연스러울 때 재귀함수를 사용합니다. 똑같은 것을 여러 번 사용하기 때문에 변수 사용이 줄어들고 가독성이 향상되어 오류가 적고, 더 좋은 코드를 적을 수 있습니다.
팩토리얼 구현
def factorial(num):
if num == 0:
return 1
else :
return num * factorial(num-1)
print(factorial(5)) # 5! = 5*4*3*2*1 = 120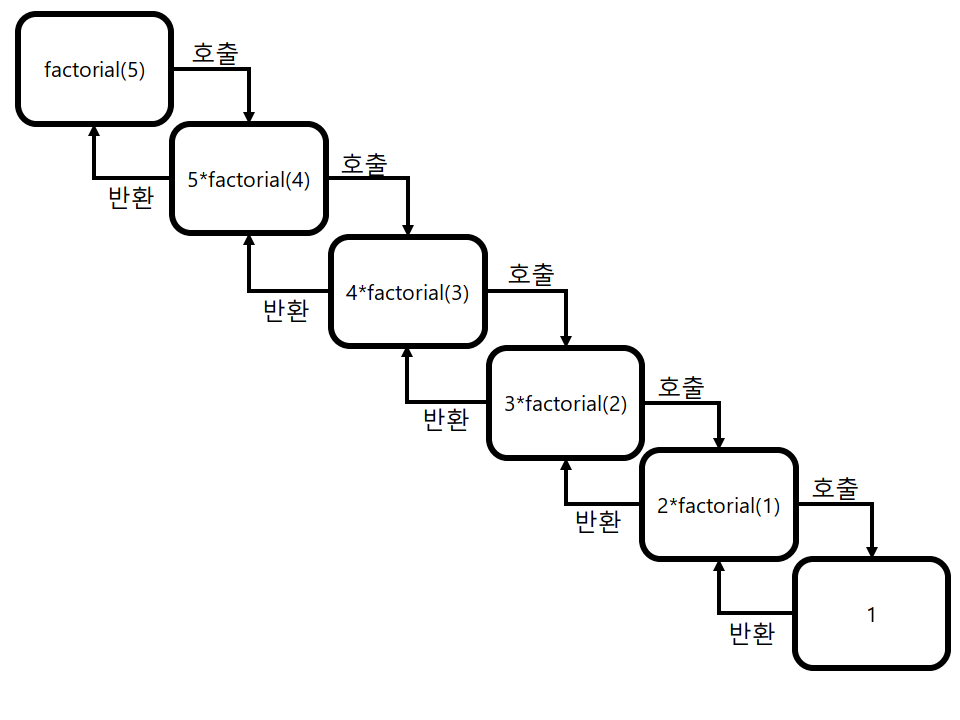
팩토리얼은 자신보다 작은 자연수를 곱하는 연산기호입니다. 5! = 5*4*3*2*1이라는 결과가 나옵니다. 해당 결과를 조금 바꾸어 보면 5! = 5*4!이라는 결과도 나올 수 있습니다. 해당 방식으로 재귀함수를 구현하였고 각각의 결과를 반환하여 120이라는 결과를 도출하였습니다. 해당 형식처럼 재귀함수를 사용하여 반복되는 형식을 계속 사용할 때 쉽게 이용할 수 있습니다.
하노이탑 구현

def hanoi(floor,from2,to):
if floor==1:
print(f"From: {from2} >> To: {to}")
else :
assist = 6 - from2 - to #보조 기둥 선정
hanoi(floor - 1, from2, assist)
print(f"From: {from2} >> To: {to}")
hanoi(floor - 1, assist, to)
floor = int(input()) #하노이탑 원반의 개수
start_locate = int(input()) #시작 위치
end_locate = int(input()) #종료 위치
hanoi(floor,start_locate,end_locate)하노이탑의 규칙은 다음과 같습니다.
- 원반은 위에서부터 꺼낼 수 있다.
- 한 번에 한 개씩 이동하여야 한다.
- 항상 작은 원반이 위에 있어야 한다.
해당 규칙에 따 3가지 경우의 수를 두었습니다.
첫 번째로 하나의 원반만 있는 경우입니다.

1층 원만 사용하는 경우에는 출발 지점과 목적지점으로 이동하면 됩니다. 이것을 소스 코드로 표현하자면 아래와 같습니다.
print(f"From: {from2} >> To: {to}")
두 번째로 두 개의 원반이 있는 경우입니다.
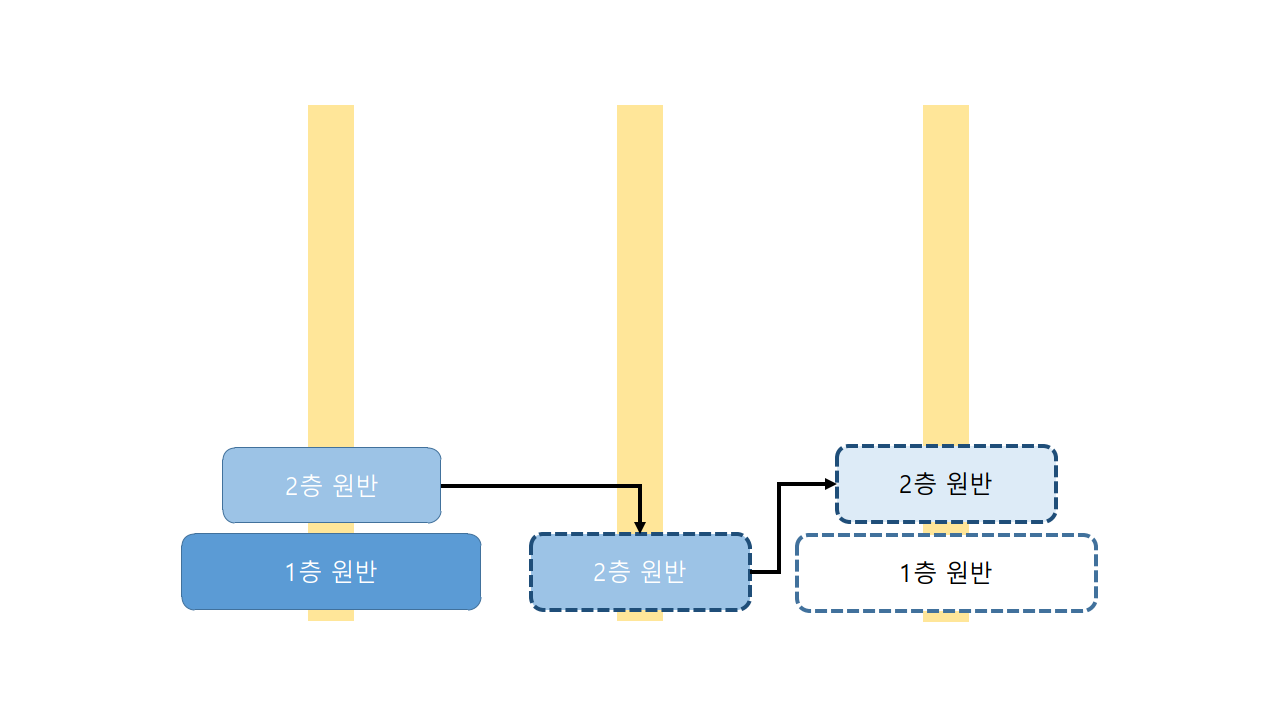
원반이 여러 개가 있는 경우에는 '항상 작은 원반이 위에 있어야 한다.'라는 규칙으로 인하여 보조 기둥을 이용하여야 합니다. 따라서 보조기둥을 이용하여 2층 원반을 두고 1층으로 두어야 합니다.
print(f"From: {from2} >> To: {assist}") #2층 원반 이동
print(f"From: {from2} >> To: {to}") #1층 원반 이동
print(f"From: {assist} >> To: {to}") #2층 원반 이동
마지막으로 여러 개의 원반이 있는 경우입니다.
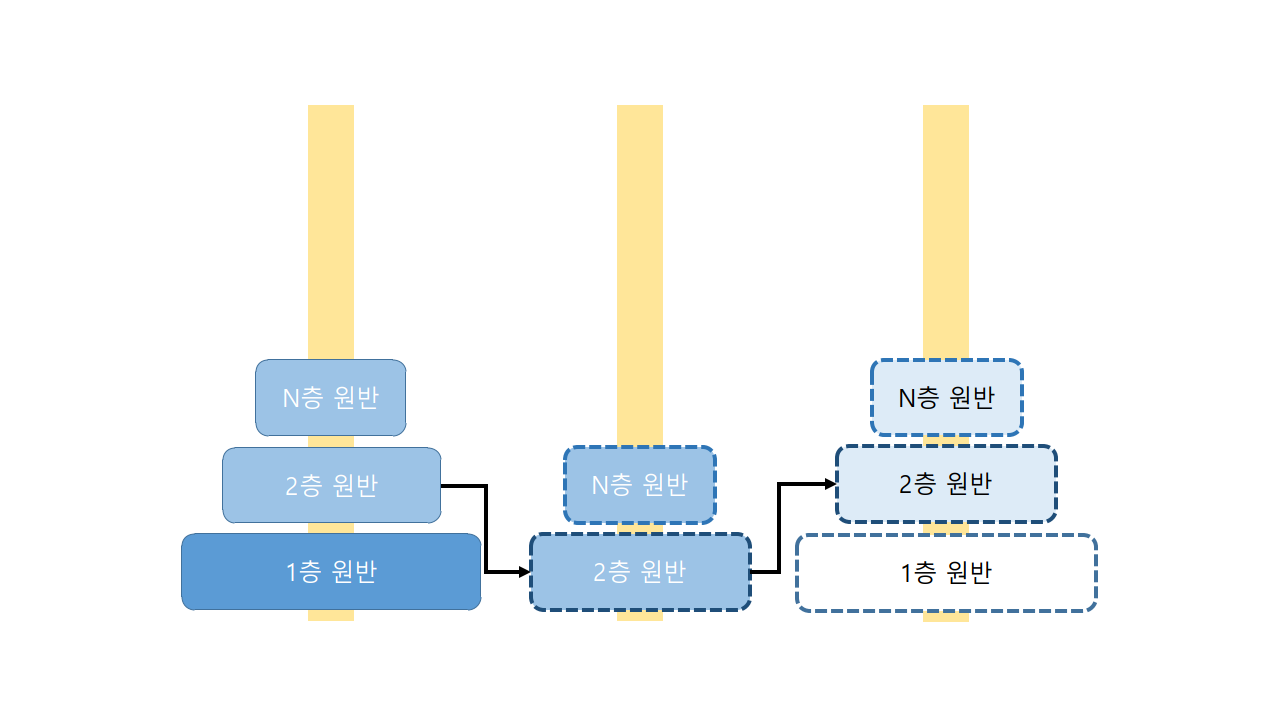
2층 원반을 통하여 알 수 있는 것은 1층 원반을 이동시키기 위해서는 2층 위에 있는 모든 원반이 보조 기둥으로 이동하여야 한다는 점입니다. 그렇게 하면 1층 원반을 이동시킬 수 있습니다. 그리고 2층 원반을 이동시키기 위해서는 또 다른보조 기둥에 3층 위에 있는 모든 원반이 있어야 한다는 점까지 알수 있습니다. 해당 방식을 재귀적으로 해결할 수 있습니다.
- 2층부터 N층까지 보조 기둥으로 이동한다
- 1층의 원반을 이동한다
- 보조기둥에 있는 원반을 도착점으로 이동한다
해당 방법을 아래의 소스 코드로 나타낼 수 있습니다.
def hanoi(floor,from2,to):
assist = 6 - from2 - to
hanoi(floor - 1, from2, assist)
print(f"From: {from2} >> To: {to}")
hanoi(floor - 1, assist, to)'floor - 1'을 한 이유는 2층부터 N층까지를 나타내기 위함입니다.
마지막으로
재귀함수를 통하여 수학적인 패턴이 계속되는 경우 쉽게 해결 할 수 있습니다.
'컴퓨터 > Python' 카테고리의 다른 글
| Python (14) - Tic-Tac-Toe게임을 만들어보자 (pygame) (0) | 2023.02.14 |
|---|---|
| Python (13) - 파이썬으로 QR코드를 만들어보자 (qrcode) (0) | 2023.02.09 |
| Python (11) - 스택(Stack)과 큐(Queue) 구현하기 (0) | 2023.01.09 |
| Python (10) - pytesseract를 이용하여 이미지 안에 있는 글자를 뽑아보자 (0) | 2023.01.07 |
| Python (9) - BeautifulSoup를 이용하여 디시인사이드에 웹 크롤링을 해보자 (4) | 2023.01.03 |