알고리즘 - 빅오 표기법 (Big-O notation)

알고리즘에 관하여 공부하다 보면 효율성을 계산해야 할 때가 많습니다. 어떻게 짜야지 속도가 더 빠른가 이런 부분으로 계산하는 데 자주 사용되는 방법인 빅오 표기법에 대하여 설명하고자 합니다.

 

빅오 표기법(Big-O notation)

Alternative big o notation algorithm T-Shirt

출처 : https://www.amazon.com

빅오(Big-O) 표기법은 알고리즘의 시간 복잡도나 공간 복잡도를 표현할 때 표기하는 방법입니다. 일반적으로 최악의 경우 성능을 평가합니다. 이를 통해 알고리즘이 얼마나 많은 시간 혹은 메모리를 사용할지를 나타냅니다. 빅오 표기법을 통하여 효율성을 비교하고 알고리즘의 성능이 어떻게 변하는지 예측할 수 있습니다.

• 시간 복잡도(Time Complexity) - 알고리즘의 입력에 따른 작업을 완료하는데 소요되는 시간
• 공간 복잡도(Space Complexity) - 알고리즘의 입력에 따라 사용하는 메모리양

빅오 표기법을 이용하여 알고리즘에 대한 성능 예측을 할 수 있으며, 두 알고리즘의 효율성을 비교할 수 있습니다. 

 

자주 사용되는 복잡도 유형

Big-O 표기법에 대한 그래프

여기서 가로축은 처리, 세로축은 실행입니다.

1. O(1): 상수 시간 복잡도. 입력 크기에 상관없이 실행 시간이 일정합니다. (stack에서 push, pop)
2. O(log n): 로그 시간 복잡도. 입력 크기가 커져 실행 시간은 아주 천천히 증가합니다. (이진 트리)
3. O(n): 선형 시간 복잡도. 입력 크기에 비례하여 실행 시간이 증가합니다. (순차 탐색)
4. O(n log n): 형 로그 시간 복잡도. 대부분의 효율적인 정렬 알고리즘이 해당합니다. (Quick Sort, Merge Sort)
5. O(n²): 2차 시간 복잡도. 중첩된 반복문을 사용하는 알고리즘에서 나타납니다. (Bubble Sort, Insection Sort)
6. O(2^n): 지수 시간 복잡도. 입력 크기가 커질수록 두 배로 실행 시간이 증가합니다.(피보나치 수)
7. O(n!): 팩토리얼 시간 복잡도. 모든 경우를 탐색할 때 발생하며 시간이 급격히 증가합니다.(순열)

복잡도 유형에 따른 실행 시간은 다음과 같습니다. 

O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2^n) < O(n!)

여기서 O(1)로 갈수록 더 빠르며 효율적인 알고리즘입니다.

 

규칙

상수항 무시

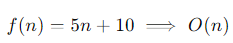
입력 크기가 크다고 가정하고 있기 때문에 상수항인 10은 무시합니다.

 

계수 무시

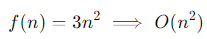
상수 계수인 3도 무시되므로 n^2으로 표기합니다.

 

최고차항만 표기

빅오표기법은 입력 크기에 따라 영향을 받기 때문에 가장 큰 항인 n^2 이외의 항들은 무시합니다

 

Reference

https://jettstream.tistory.com/113

빅-오(Big-O) 표기법

https://web.mit.edu/16.070/www/lecture/big_o.pdf